My First Fluids Case: cylinderInChannel
Case Overview
Running our first fluid case: cylinderInChannel
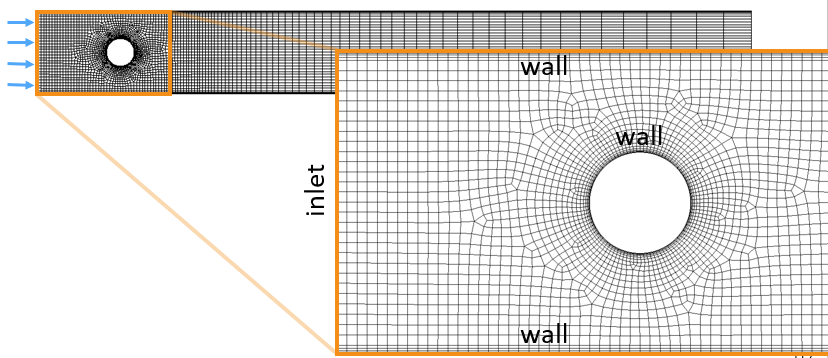
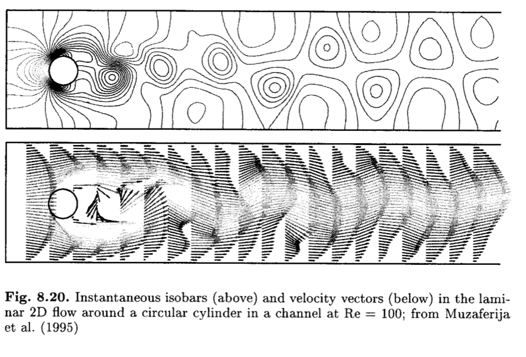
This is the classic “flow over a cylinder in a channel” test case, as analysed by, for example, Ferziger and Peric (2002). The problem is modelled as 2-D.
The inlet flow velocity profile is specified (coming in from the left) and the outlet (right) gauge pressure is zero.
The upper wall, lower wall and cylinder are no slip walls.
Expected Results
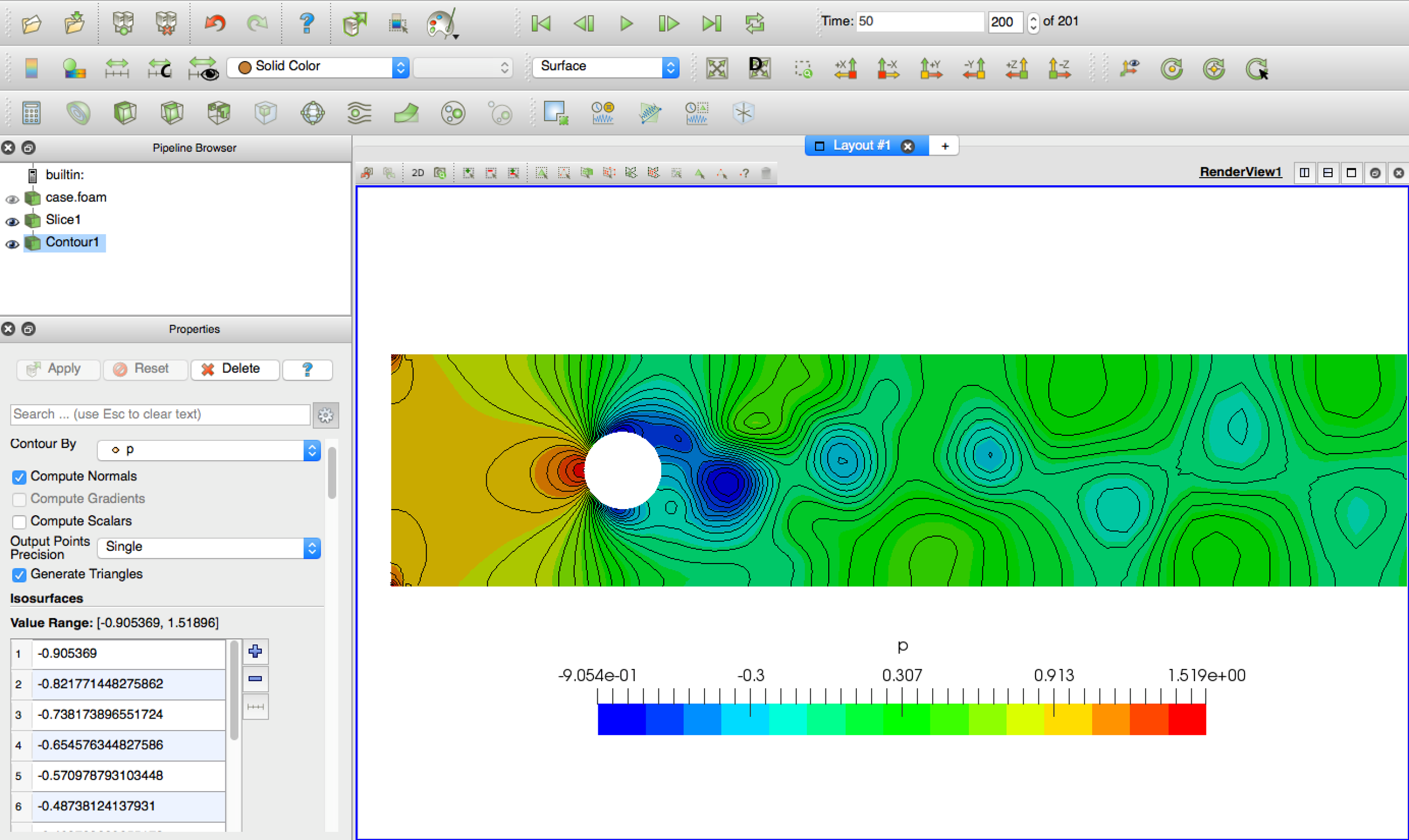
For Re = 100, the flow is expected to be unsteady with vortices shedding from the cylinder.
Theory
We assume an incompressible Newtonian isothermal laminar fluid, where the Navier-Stokes governing equations take the form:
Theory: solution methodology
In this case, we will use a transient version of the SIMPLE algorithm (e.g. pimpleFoam); we could have also used PISO or a coupled approach.
for all time-steps
do
solve momentum equation for U (terms depending on
p are calculated explicitly)
solve pressure equation for p (terms depending on
U are calculated explicitly)
while not converged
end
Running the Case
Running our first fluid case: cylinderInChannel
Change directory into the cylinderInChannel tutorial case:
$> cd $FOAM_RUN/tutorials/fluids/cylinderInChannel
Or if using the docker image:
$> cd $FOAM_RUN/../sharedRun/tutorials/fluids/cylinderInChannel
We can run the case using the Allrun script, or manually (using the commands from the Allrun script):
$> fluentMeshToFoam cylinderInChannel.msh
$> changeDictionary
$> solids4Foam
We will now look at the results in ParaView:
$> paraFoam # or “paraFoam -nativeReader”
$> # or “touch case.foam && paraview case.foam”
Let us examine the cylinderInChannel case structure and discuss the similarities and differences between a “fluid” case and a “solid” case
cylinderInChannel
├── 0
│ ├── U
│ └── p
├── Allclean
├── Allrun
├── constant
│ ├── RASProperties
│ ├── dynamicMeshDict
│ ├── fluidProperties
│ ├── physicsProperties
│ ├── polyMesh
│ │ └── …
│ ├── transportProperties
│ └── turbulenceProperties
├── cylinderInChannel.msh
└── system
├── changeDictionaryDict
├── controlDict
├── fvSchemes
└── fvSolution
-
The case setup is the same as a typical “simpleFoam/pimpleFoam” case, apart for a couple of small differences.
physicsProperties: in this case, we specify the analysis type to be “fluid”:
type fluid; //type solid; //type fluidSolidInteraction; - For a fluid analysis, we must specify the type of fluid model in the fluidProperties dictionary; in this case we will use a transient SIMPLE approach for a incompressible isothermal fluid:
fluidModel transientSimpleFluid; transientSimpleFluidCoeffs { nOuterCorrectors 200; nNonOrthogonalCorrectors 0; pRefCell 0; pRefValue 0; convergence 1e-7; } - Apart from specifying the physicsProperties and fluidProperties dictionary, the case is equivalent to standard OpenFOAM fluid cases, e.g. specifying transportProperties, RASProperties, dynamicMeshDict, U, p, fvSchemes, etc.
Case Settings
cylinderInChannel
├── 0
│ ├── U
│ └── p
├── Allclean
├── Allrun
├── constant
│ ├── RASProperties
│ ├── dynamicMeshDict
│ ├── fluidProperties
│ ├── physicsProperties
│ ├── polyMesh
│ │ └── …
│ ├── transportProperties
│ └── turbulenceProperties
├── cylinderInChannel.msh
└── system
├── changeDictionaryDict
├── controlDict
├── fvSchemes
└── fvSolution
- Settings for the solution algorithm (e.g. SIMPLE or PISO) are specified in the fluidProperties dictionary (as opposed to the fvSolution) dictionary:
transientSimpleFluidCoeffs { nOuterCorrectors 200; nNonOrthogonalCorrectors 0; pRefCell 0; pRefValue 0; convergence 1e-7; }
Code
cylinderInChannel: code
As discussed in the hotSphere solid tutorial case slides, the solids4Foam solver creates a run-time selectable physicsModel; in the case, we have selected this to be the transientSimpleFluid model.
The code for the transientSimpleFluid class is located at: solids4foam/src/solids4FoamModels/fluidModels/transientSimpleFluid/transientSimpleFluid.C
Let us examine the “evolve” function of this class to see the equations solved…
bool transientSimpleFluid::evolve()
{
if (consistencyByJasak_)
{
return evolveConsistentByJasak();
}
else
{
return evolveInconsistent();
}
}
bool transientSimpleFluid::evolveInconsistent()
{
Info<< "Evolving fluid model" << endl;
const fvMesh& mesh = fluidModel::mesh();
const int nNonOrthCorr =
readInt(fluidProperties().lookup("nNonOrthogonalCorrectors"));
const int nOuterCorr =
readInt(fluidProperties().lookup("nOuterCorrectors"));
scalar convergenceCriterion = 0;
fluidProperties().readIfPresent("convergence", convergenceCriterion);
// Prepare for the pressure solution
label pRefCell = 0;
scalar pRefValue = 0.0;
setRefCell(p(), fluidProperties(), pRefCell, pRefValue);
phi().oldTime();
for (int oCorr = 0; oCorr < nOuterCorr; oCorr++)
{
scalar eqnResidual = 1, maxResidual = 0;
p().storePrevIter();
if (mesh.moving())
{
// Make the fluxes relative
phi() -= fvc::meshPhi(U());
}
// Calculate CourantNo
{
scalar CoNum = 0.0;
scalar meanCoNum = 0.0;
scalar velMag = 0.0;
fluidModel::CourantNo(CoNum, meanCoNum, velMag);
}
// Construct momentum equation
fvVectorMatrix UEqn
(
fvm::ddt(U())
+ fvm::div(phi(), U())
+ turbulence_->divDevReff()
);
UEqn.relax();
// Solve momentum equation
eqnResidual =
solve(UEqn == -gradp()).initialResidual();
maxResidual = max(eqnResidual, maxResidual);
volScalarField aU = UEqn.A();
U() = UEqn.H()/aU;
phi() = (fvc::interpolate(U()) & mesh.Sf());
# include "adjustPhi.H"
for (int nonOrth = 0; nonOrth <= nNonOrthCorr; nonOrth++)
{
// Construct pressure equation
fvScalarMatrix pEqn
(
fvm::laplacian(1/aU, p()) == fvc::div(phi())
);
// Solve pressure equation
pEqn.setReference(pRefCell, pRefValue);
pEqn.solve();
if (nonOrth == nNonOrthCorr)
{
phi() -= pEqn.flux();
}
}
// Calculate Continuity error
fluidModel::continuityErrs();
// Explicitly relax pressure for momentum corrector
p().relax();
gradp() = fvc::grad(p());
U() -= gradp()/aU;
U().correctBoundaryConditions();
turbulence_->correct();
if (maxResidual < convergenceCriterion)
{
Info<< "reached convergence criterion: "
<< convergenceCriterion << endl;
Info<< "Number of iterations: " << oCorr << endl;
break;
}
}
return 0;
}